Diversas culturas a lo largo de la historia, se interesaron en el diseño de figuras geométricas, que de manera individual o combinada, utilizaban para cubrir alguna superficie plana sin dejar espacios, como una forma de decoración de interiores y exteriores de casas y templos:
“El diseño de figuras geométricas que individualmente o en combinación cubren una superficie plana sin “baches” se remonta a la antigüedad. Los sumerios (cerca del 4.000 a. de C.) en el Valle del Mesopotam construyeron casas y templos decorados con mosaicos con patrones geométricos” (Bonilla, Espinosa, Feria & Martínez, 2007, p. 50).
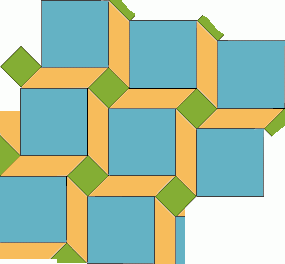
Para lograr cada una de estas creaciones artísticas, emplearon simetrías, traslaciones y rotaciones de figuras geométricas que se manifestaron en frisos y mosaicos geométricos, utilizando diferentes tipos de materiales. Sin embrago, uno de los más grandes exponentes contemporáneos de estas producciones artísticas y del arte matemático es el holandés Maurits Cornelius Escher, quien desarrolló el método de las teselaciones para dividir regularmente la superficie plana, que sería admirado por cristalógrafos y matemáticos. En nuestro mundo, son muy variados los escenarios, expresiones y situaciones en los que se manifiestan las teselaciones, como por ejemplo, el embaldosinado de pisos. Ya en el dominio del conocimiento matemático, la palabra teselación o embaldosinado hace referencia al uso repetido de polígonos u otras figuras curvas que llenan completamente una región plana infinita sin vacíos ni superpuestos (Bonilla, Espinosa, Feria & Martínez, 2007, p. 50), “es el cubrimiento completo de un plano mediante una o más figuras en un patrón repetido, con ninguna figura superpuesta” (Bonilla, Espinosa, Feria & Martínez, 2007, p. 56), como por ejemplo:
Teselación o Mosaico Geométrico
Es importante resaltar que las teselaciones dependiendo de los polígonos o figuras utilizadas en el cubrimiento del plano, se clasifican en Teselaciones Poligonales, es decir, aquella “teselación formada completamente por polígonos: triángulos, cuadriláteros, hexágonos…” (Bonilla, Espinosa, Feria & Martínez, 2007, p. 57).
Teselaciones con cuadriláteros
También existen las Teselaciones regulares que se construyen con polígonos regulares, es decir, aquella figura cuyos lados y ángulos tienen la misma medida. “Una teselación es regular si está formada por polígonos regulares congruentes. Sólo tres polígonos regulares pueden formar teselaciones regulares. Estos son: 1. Un triángulo equilátero; 2. Un cuadrado; y 3. Un Hexágono regular” (Bonilla, Espinosa, Feria & Martínez, 2007, p. 58).
Teselaciones con Hexágonos
Las teselaciones también pueden ser semirregulares, es decir, aquellas que “combinando dos o más polígonos regulares para teselar un plano” (Bonilla, Espinosa, Feria & Martínez, 2007, p. 59).
Teselaciones semiregulares
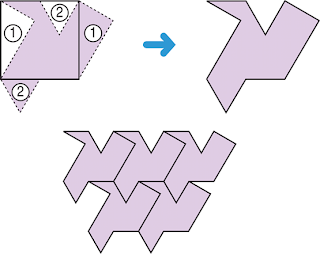
Pero además, las teselaciones pueden ser poligonales no regulares, cuando se tesela el plano con figuras que se desprenden de un polígono regular por efecto de la técnica del mordisco, que consiste en cortar en uno de los lados del polígono algún tipo de figura (como se muestra a continuación), la cual mediante deslizamientos, giros y reflexiones se ubica en el lado opuesto al corte, dando origen a la tesela o loseta generado de producciones artísticas.